Induktivní statistika

1. Statistika jako opora vědecké metody

V přírodních vědách, medicíně stejně jako v sociálních vědách využívajících empirických pozorování a měření, se dospívá k obecným závěrům v souladu s vědeckou metodou. Její postup se dá fázovat do následujících kroků.

Formulace problému
Formulace hypotézy (jako dílčí části problému)
Návrh experimentu nebo šetření (s cílem získání dat)
Získání dat obsahujících informaci relevantní pro ověření hypotézy
Volba či návrh statistické metody, která by umožnila verifikovat oprávněnost hypotézy konfrontací s daty
Vyvození závěru o hypotéze (jako příspěvek k řešení problému)

Účast statistiky, případně statistika, se předpokládá ve fázi formalizace problému a formulace hypotéz, dále ve fázi plánování pokusu či šetření (sběru dat) a zejména při zpracování, hodnocení dat, ověřování hypotézy a vyvozování závěrů o její event. platnosti. V této druhé části musí být respektována zejména povaha dat: metoda statistické analýzy musí brát v úvahu, jde-li o data nominální, ordinální nebo metrická, jak je podrobněji popsáno jinde.

Je třeba mít na zřeteli, že ani sebevíc sofistikovaná, rafinovaná a vynalézavá procedura statistické analýzy (odhadování parametrů či testování hypotéz) nedokáže dát smysl studii, v níž byly hrubě zanedbány zásady reprezentativnosti a znáhodňování při pořizování dat, případně narušeny požadavky objektivnosti, validity a reliability měření. Tato rizika a nebezpečí jsou aktuální dnes víc než dříve, protože jakékoli statistické výpočty jsou poměrně snadno dosažitelné ve statistických softwarových balících.

Ad 1. Problémy, které mají být řešeny, vystupují jen málokdy samy od sebe v explicitní formě. Právem platí, že ten, kdo dokázal v dané situaci nápaditě „vyhmátnout“, oč vlastně jde a „vyloupnout“ jádro, podstatu věci, už svou úlohu napůl vyřešil. Nikdy by se proto nemělo litovat času věnovaného rozboru situace, identifikaci struktury úlohy, diagnostice problému. V této věci platí, že výhodu mají ti, kdo jsou se situací dobře obeznámeni, kdo mají s ní předchozí zkušenost. Pozdější řešení úlohy bude komplikováno nejasným vymezením struktur a parametrů situace, veličin, znaků a ukazatelů v ní vystupujících. Jednoduchost je heslo dne, přehledné uchopení reality má prioritu. Složité modely mohou být působivé; je však škodlivé zapomínat, že se složitostí modelu rostou nároky na jeho číselnou specifikaci. Složitost modelu by měla odpovídat možnostem empirického měření a pozorování. Souvisí to často s řešitelností problému vůbec.

I ta nejsložitější teoretická koncepce je zjednodušením reálné skutečnosti. Podstatné je, aby badatel už v počáteční fázi zkoumání situace rozpoznal, které z intervenujících proměnných je nezbytné v modelu podržet, a které je možno- alespoň v prvním přiblížení- ze sledování vypustit. Nadměrný ohled na detail může zavalit jádro problému hlušinou ztěžující pochopení hlavních tendencí a principů.

Ad 2. Vědecké usuzování je řetězem logických- deduktivních a induktivních- kroků. Badatel má zpravidla určitou intuitivní (zkušeností podloženou) představu o mechanismech, které v uvažované situaci hrají roli- a tu „podsouvá“ zkoumané realitě jako možné vysvětlení jejího chování. Právě takhle jednáme s hypotézami, jejichž „přijatelnost“ pro explikaci chování systému chceme verifikovat. Touhle konstrukcí vytváříme umělý, (artificiální) svět, oživujeme určitou (ve světle naší zkušenosti oprávněnou) fikci, jakousi „podmíněnou“ realitu.

Hypotéza by měla být formulována jasně. Měla by se dovolávat zřetelně, smysluplně a jednoznačně zavedených pojmů. Hypotéza má postulovat vztah mezi premisami a důsledky- a to tak, že to umožňuje ověření její platnosti statistickými technikami prostřednictvím empirické informace obsažené v datech. Pokud je hypotéza držena jako plauzibilní, musí být schopna sloužit jako nástroj predikce chování sledovaného systému. Zřetelně artikulovaná hypotéza umožňuje konfrontaci aktuálních představ badatele s tím, jak byl a jak je problém pojednáván v dostupné literatuře.

Experimentální hypotéza umožňuje, aby byla na jejím základě odvozena tzv. nulová hypotéza, která bude vlastním objektem statistické verifikace.

Ad 3. Plán pokusu nebo šetření zahrnuje seznam veličin (znaků, charakteristik), jejichž souhrn má popisovat chování systému. Pokusným plánem je třeba vymezit faktory, které mohou chování systému měnit a které mají být proto pod kontrolou experimentu anebo mají být alespoň evidovány. S každou sledovanou veličinou je specifikován její typ a způsob jejího měření, včetně jednotek a kategorií příslušných škál.

Plán pokusu definuje statistickou jednotku, na níž se měří či pozoruje (objekt, subjekt) a způsob pořízení výběru (vzorku) z příslušné referenční populace statistických jednotek. Vzetí vzorku musí garantovat jeho reprezentativnost vzhledem k referenční populaci, čehož se dosahuje náhodným mechanismem vybírání. Spolehlivost závěrů je přitom určována především dostatečným rozsahem výběru.

Náhodnost vybírání statistických jednotek do vzorku znamená, že každý prvek populace má mít stejnou šanci být do vzorku zahrnut.

Ad 4. Základním problémem, se kterým se musí sběr dat potýkat, je vyhnout se všem systematickým chybám a regulovat, jak jen je to možné, velikost chyb náhodných. Znamená to- udržovat zdroje systematických chyb pod kontrolou, vyvažovat působení možných vlivů na sledované znaky a veličiny. V sociálním, politickém šetření je takových zdrojů nepočítaně, což činí získávaná data „měkkými“(soft).

Jedním ze způsobů kontroly je posuzování odlehlých dat (outliers)- a jejich případné vyloučení ze souboru.

Ad 5. Volba statistické metody vhodné k řešení úlohy je problém klíčový. V zásadě jde vždycky o to, formulovat nulovou hypotézu jako jádro řešeného problému a pak posoudit, zdali je data možno přijmout jako očekávaný důsledek platnosti hypotézy- a případné pochybnosti jsou vysvětlitelné a zdůvodnitelné působením pouze náhodných vlivů. Není-li tomu tak, nulová hypotéza se zamítá jako nepřijatelná- a hledá se alternativní vysvětlení. Zvolená statistická technika, pomocí níž se počítá signifikance a rozhoduje o eventuálním zamítnutí hypotézy, musí respektovat typ dat a další okolnosti, za nichž byla data pořizována.

Ad 6. O závěru vyvozeném z dat- v záležitosti testované hypotézy- rozhoduje případná signifikance výsledku, resp. tzv. „tail probability“, tj. pravděpodobnost, že by bylo možno za platnosti nulové hypotézy dostat výsledek alespoň tak jí nepříznivý, jako je výsledek aktuálně pozorovaný.

Důležité je kontrolovat, aby se experimentální interpretace nálezu „držela“ interpretace statistické a „nešla“ za oblast jejího přenosu. Neoprávněné rozšíření statistického nálezu bývá poměrně častou chybou při interpretaci statistického závěru.

Účast statistiky ve vývoji vědecké metody má svou prehistorii, jdoucí před objev teorie statistického testování. Statistická indukce a její paradigma (data jsou pouze výběrem, vzorkem z referenční populace, na niž se mají nálezy zobecnit) „byly ve vzduchu“ už před začátkem 20. století, před dobou, od níž se teoriestatistické indukce začala systematicky odvíjet.

Zmíníme se jenom o jednom momentu, který má své místo v dějinách české a evropské vědy.

T.G.M. a teorie indukce

V polovině 18. století se kriticky zamýšlel anglický filozof David Hume nad omezeností poznání opřeného o empirická pozorování. Hume konstatuje, že jenom ve vědách deduktivních, jako jsou matematika a logika, je pravdivost zákonů (vyvozovaných z výchozích axiomů) jednoznačně verifikovatelná: nebude-li v řetězu úvah od pravdivé premisy k závěru učiněn chybný krok, bude i závěr pravdivý. Pokud jde o vědy, vycházející z empirických pozorování, je Hume v otázce pravdivosti vyvozovaných závěrů skeptický: protože seberozsáhlejší soubor pozorování není vyčerpávající, není tu ani absolutní jistota, že dalšími novými pozorováními nebude učiněný závěr vyvrácen.

Na podzim 1882 nastupoval Tomáš Garrigue Masaryk, tehdy soukromý docent univerzity ve Vídni, na místo profesora filozofie univerzity v Praze. Uvedl se přednáškou Počet pravděpodobnosti a Humova skepse, která v lednu následujícího roku 1883 vyšla tiskem pod týmž názvem s podtitulem Za historický úvod v theorii indukce.

Masarykův komentář ke Humově chápání pojmu příčiny a následku se dá shrnout takto (TGM se opíral o Humův spis An Inquiry Concerning Human Understanding, 1748).

Jednotlivá, izolovaná zkušenost, jež pozoruje následnost dvou jevů, nedává právo formulovat obecné pravidlo předpovědi. Teprve tehdy, když pokaždé za stejných okolností tyto dva po sobě následují, jsme oprávněni z objevení se jednoho usuzovat, že se i druhý jev objeví. První jev pak nazveme příčinou a druhý důsledkem a předpokládáme, že mezi nimi existuje spojitost- a hledáme sílu, která ono následování působí.

Pojem souvislosti tedy odvozujeme od zkušenosti pozorované v mnoha podobných situacích. Souvislost se upevňuje opakováním zkušenosti. Příčina je jevem, po němž následuje jiný jev, s tím, že jevy podobné prvému jsou následovány jevy podobnými jevu druhému. Příčina je to, co kdyby nebylo, nebylo by důsledku.

V matematice se vztahy příčiny a důsledku dokazují logicky, bez odkazu na smyslovou zkušenost.

Ve světě reálně existujících věcí je tomu jinak. Vztahy příčiny a účinku (důsledku) nepoznáváme rozumově, ale smyslově, zkušeností.Matematika v tom nepomůže. Všechno, co odvozujeme ze zkušenosti, zakládá se na podobnosti. A priori soudíme, že vztahy mezi jevy zůstanou v budoucnu stejnými, jakými byly v minulosti, a že podobné síly vyvolávají podobné účinky. Tento poslední názor není získán zkušeností, je to princip apriorně nám daný.

Jde o princip zvyku, přirozeně člověku vrozený. Jím překračujeme meze smyslového vnímání i meze paměti; na druhé straně však musí naše smysly či paměť zprostředkovat nějakou událost jako podnět k uvažování o příčině a účinku resp. jejich řetězu.

Do příčinné souvislosti věcí nevnikáme rozumem. K tomu nás obdařila příroda jakýmsi pudem, mechanickým návykem. Tak byla apriorně zjednána jistá zvláštní harmonie mezi během přírody a souvislostmi našich pojmů.

Rozum a zkušenost se navzájem vylučují-li to je esence Humovy skepse. Jen v matematice si můžeme být jisti nade všechnu pochybnost. Ostatní vědy, založené na zkušenosti, jsou nejisté, protože příčinnou souvislost postihují jen neúplně.

„Tyto Humovy myšlenky rozbouřily filosofy tou měrou, že podnes záhady pojmu příčinnosti definitivně nejsou rozřešeny“- praví Masaryk.-Přírodověda, jíž týkala se ta skepse nejvíce, nedala se másti Humovými výroky, a berouc se prostě tou „nejistou“ indukcí, došla úspěchů, které snad s to jsou i nejzarytějšího skeptika v pochybnost uvésti. Avšak úspěchy přírodovědné logickým odčiněním Humových námitek nejsou.“

Masaryk poté shrnuje svůj názor:

Existují i logické důvody, proč nepřijímat Humovu skepsi. Nejen matematika, ale i vědy opírající se o zkušenost, mohou stupeň své jistoty specifikovat, a to prostřednictvím počtu pravděpodobnosti. Pravděpodobnostně se nevysvětluje povaha příčinnosti- je však možné to, co zdravý rozum spatřuje mechanismem zvyku (tohle Hume viděl správně), formulovat vědecky. Zde Masaryk cituje Laplacea, podle něhož pravděpodobnost není nic jiného než zdravý rozum převedený do řeči čísel. Humovu skepsi je pak možno chápat jako nedocenění, nerozpoznání rozdílu mezi důvěrou (v existenci vztahu mezi jevy) subjektivní a matematicky kvantifikovatelnou důvěrou objektivní.

Problém induktivního usuzování v empirických vědách (kam patří nejen přírodní vědy, ale i lékařství, technická experimentování, zemědělské pokusnictví, psychologický a sociální výzkum) nastoupil krátce poté, co se jím Masaryk zabýval ve své inaugurační přednášce, bouřlivý rozvoj.

Začátkem našeho století podněcuje kontakt matematiky s britským biologickým výzkumem vznik prvotní ideje statistického testu jako metody, v níž je indukce verifikující hypotézu řízena tím, že se předem stanovuje riziko jejího neoprávněného zamítnutí. Tato tzv. signifikance testu je dnes odborným termínem ve slovníku každé empirické vědy a její standardní velikost 0,05 = 1/20 patří ke všeobecnému vzdělání.

Silnou inspirací se rozvoji statistické indukce stala kontrola jakosti v případě destrukčních zkoušek- zejména střeliva a dělostřeleckých nábojů- za 2. světové války.

Na Humovu skepsi dnes odpovídá celý vědní obor- matematická statistika- jejímž programem je právě navrhování a studium vlastností matematických modelů induktivního usuzování: v posledních desetiletích je dosah aplikace induktivních statistických metod násoben existencí výkonných výpočetních systémů- kdy jsou statistické softwarové balíky běžně instalovány v podstatném procentu všech PC.

2 Statistické odhadování

Statistika se zabývá jenom masovými, hromadnými jevy a veličinami, u nichž lze předpokládat opakovatelnost pozorování a měření. To znamená, že ke každému souboru dat si lze představit jiný soubor dat, pořízený dalším výběrem z referenční populace. Zkušenost získaná v situacích, kdy se taková opakovaná měření a opakované pořizování datových souborů opravdu konají, nás učí, že se takové datové soubory vzájemně liší. V důsledku toho se liší i charakteristiky na souboru dat počítané, jako jsou např. průměr znaku či frekvence výskytu nějakého jevu.

Tato zkušenost odůvodňuje, proč postuluje základní statistické paradigma existenci teoretické, koncepční, často jen virtuálně existující referenční populace- a soubory dat, jak se běžně pořizují, považuje za vzorky, výběry z populace. Statistická indukce z výběru na populaci je pak prováděna za předpokladu, že výběry byly pořizovány náhodně, což má zaručovat reprezentativnost výběru vzhledem k populaci. Výběr je tedy náhodný, jestliže měl každý prvek referenční populace stejnou možnost být do výběru zahrnut. Obtížná realizovatelnost čistě náhodného vybírání vedla k řadě modifikací tohoto principu, k nimž patří stratifikovaný výběr, systematický výběr, skupinový výběr, vícestupňový výběr.

Statistické charakteristiky počítané na výběru jsou tedy vlastně jakýmisi odhady jejich protějšků v populaci.

Příklad. Jak počítá statistik ryby v rybníku.

V rybníku je neznámý počet (označme ho N) ryb, o němž bychom se rádi něco dověděli. Metoda přímého, vyčerpávajícího měření, vyžadující, aby byl rybník vypuštěn, není přitom použitelná.

Statistik navrhuje nepřímý postup, opírající se o výběr:

Z rybníka se vyloví n ryb, které se označí a pustí do rybníka zpět. Po nějaké době (zaručující promíchání n označených ryb mezi ostatní) se provede další částečný výlov; řekněme, že při něm bylo vyloveno n₁ ryb, mezi nimiž se rozpoznalo k₁ (0 ? k₁ ? min (n₁, n)) ryb dříve označených. Přijme-li se princip, že podíl označených ve vzorku n₁ vylovených ryb se rovná podílu označených v celém rybníku, měl by platit vztah

v němž k₁, n a n₁ jsou veličiny známé, což umožňuje odhadovat počet ryb v rybníku ze vzorce

Konkrétně, jestliže například bylo označeno n = 200 ryb a mezi znovu vylovenými n₁ = 100 rybami se nalezlo k₁= 5 označených, lze se domnívat, že v rybníku žije asi

ryb.

Profesionální statistický přístup tímto výpočtem ovšem nekončí- spíše teprve začíná. Získaný výsledek N = 4000 je třeba považovat za odhad, který je vystaven riziku omylu. Bylo by přece naivně optimistické předpokládat, že v rybníku žije právě tolik ryb, kolik ukazuje náš odhad. Podstatné je, že velikost chyby (odchylky odhadu od neznámé skutečnosti) se dá rovněž statistickými metodami posoudit a ukázat její závislost na rozsahu výběru n a podílu označených ryb n/N.

Pravděpodobnostní a statistické uvažování je velmi univerzálně použitelné. Není proto divu, že existuje analogie mezi počítáním ryb a sázením do lotynky. Stačí vést podobnost mezi počtem ryb N a 49 čísly v lotynce, počtem označených ryb n₁ a šesti „šťastnými“ vyhrávajícími čísly a mezi počtem k₁ označených ryb zachycených ve druhém výlovu a počtem „uhádnutých“ šťastných čísel z vyhrávající šestice.

Z toho vyplývá, že počet k₁ označených ryb ve druhém výlovu je náhodná veličina s hypergeometrickým rozdělením

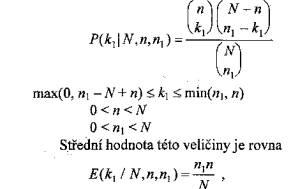
což naznačuje, že výše uvedený postup odhadování byl rozumný.

Příklad. Americký protestantský časopis Christian Herald referoval o průzkumu, při kterém byl rovněž sledován počet konvertitů od katolictví k protestantismu za posledních deset let. Respondenty dotazníků byli protestantští kněží a odpověď na tuto otázku vypovídala také o úspěšnosti jejich pastorační činnosti- kolik katolíků obrátili na protestantství.

Z celkového počtu 181 tisíc kněží bylo vybráno 25 tisíc, kterým byly rozeslány dotazníky. Vyplněných se vrátilo 2 219. Po sečtení údajů o konvertitech na nich uvedených se dostal součet 51361. Projekcí tohoto údaje (přepočtení na jednoho kněze) dalo 51 361/2 219 = 23,146 konvertitů- což představuje- pro celou kněžskou obec- odhad

23,146 × 181 000 = 4189 428

konvertitů za ono desetiletí.

Kritika tohoto údaje začíná otázkou „A co bylo asi na oněch více než 90% dotazníků (25 000- 2 219 = 22 781 celkem), které se nevrátily (a zřejmě skončily v koši)“

Střízlivá rozvaha napovídá, že je adresáti nevrátili zřejmě proto, že nemohli uvést nic, co by je stavělo do příznivého světla. Předpokládejme tedy, že by na nich byla uvedena nula.

Za tohoto předpokladu by ovšem odhad celkového počtu konvertitů získaný projekcí vypadal podstatně jinak.

Úhrn 51361 konvertitů by se měl dělit 25 000- a teprve tento údaj vynásobit počtem kněží- což by vedlo k výslednému odhadu úhrnu konvertitů, totiž

Tento údaj je zcela odlišný a podstatně střízlivější nežli údaj předchozí.

Jistou modifikací bodového odhadování, kdy je hodnota statistické charakteristiky nalezená ve výběru „prohlášena“ za příslušnou hodnotu populační, je odhadování intervalové, konstruující tzv. intervaly spolehlivosti. Jde o to, najít pomocí empirické informace obsažené ve výběru takové dvě hodnoty (dolní a horní konec intervalu příslušné škály), že interval jimi vymezený „pokryje“ s předepsanou spolehlivostí neznámou, odhadovanou hodnotu populačního parametru. Spolehlivostí se přitom rozumí pravděpodobnost, že interval odhadovanou hodnotu opravdu pokryje.

Protože ani v oblasti informace neexistuje žádné „perpetuum mobile“, resp. platí, že „prázdný pytel nestojí“, ukazuje se v konkrétních situacích, že s dostatečně vysokou spolehlivostí (ta se obvykle předepisuje na úrovni 0,95) dostáváme odhady tím určitější, tj. intervaly tím užší, čím větší je rozsah výběru, neboli čím bohatší byla empirická informace.

Současně zadaný požadavek na spolehlivost intervalového odhadu (0 < P < 1) a šířku intervalu d umožňuje pak stanovit rozsah výběru n, schopný požadavky garantovat. Názorně je tento princip demonstrován na případě odhadu populačního průměrumgaussovsky (normálně) rozděleného znaku X, kdy je hodnota parametru modhadována pomocí výběrového průměru . Platí totiž

, (3.3.1)

kde je (a/2) 100%-ní percentil standardizovaného normálního rozdělení N(0, 1) a s² je rozptyl veličiny X v referenční populaci (znalost jeho hodnoty se předpokládá).

Ostrost odhadu d je přitom rovna

z čehož se vypočítá rozsah výběru n potřebný k zajištění předepsané spolehlivosti 1-a a ostrosti d

. (3.3.2)

Platí, že při daném rozsahu empirické informace n jsou požadavky spolehlivosti a ostrosti odhadu v konfliktu: vysoce spolehlivý odhad je neostrý (neurčitý), zatímco odhad ostrý, určitý bude málo spolehlivý.

3 Co je statistický test

Statistik vyslovuje hypotézu o konceptu, o vlastnostech referenční populace. Takové tvrzení se označuje jako nulová hypotéza H₀. Týká-li se hypotéza číselné hodnoty parametru pravděpodobnostního rozdělení uvažované veličiny, nazývá se test parametrickým; v případě obecnější formulace o vlastnostech rozdělení provádí se test neparametrický. Protože nejčastěji užívanou heuristickou procedurou v empirickém výzkumu je srovnání, mívá velmi obvykle nulová hypotéza formu tvrzení, že se sledovaná veličina chová „statisticky stejně“ za různých vymezených podmínek.

Statistický test je pravidlo, určující chování badatele v případě každého z možných empirických výsledků. Protože těmito výsledky jsou (jeden nebo více) výběry z populací, musí test ke každé možné „konstelaci“ výběrového prostoru přiřadit jedno ze dvou rozhodnutí: buď (a) podržet nulovou hypotézu jako plausibilní (protože pozorování jsou v přijatelném souladu s tím, co se za platnosti nulové hypotézy očekávalo), anebo (b) zamítnout nulovou hypotézu jako (ve světle empirických dat) nepřijatelnou- a přijmout místo ní konkurenční, alternativní hypotézu. Výsledek (b) se označuje jako signifikantní; ta část výběrového prostoru, která vede k signifikantnímu výsledku, se označuje jako kritický obor testu.

Statistická indukce realisticky připouští, že i v případě platnosti nulové hypotézy může test tuto zamítnout, což se označuje jako chyba 1. druhu. Její riziko se měří pravděpodobností, že k takové chybě dojde; obvyklý požadavek na kontrolu rizika chyby 1. druhu kladený bývá roven 0,05- a označuje se termínem signifikance testu.

Se statistickým testem jako rozhodovací procedurou je spojeno ještě jiné riziko, resp. celá škála rizik. Platnou může být některá z celé množiny alternativních hypotéz- a test jako rozhodování činěné za přítomnosti náhody může připustit platnost nulové hypotézy i tehdy, platí-li ve skutečnosti některá z alternativ. Tento jev se označuje jako chyba 2. druhu a riziko s ním spojené se měří pravděpodobností výskytu této chyby.

Celou situaci zachycuje schéma:

Neznámá skutečnost	Rozhodnutí testu
Neznámá skutečnost	podržet H₀	zamítnout H₀
H₀ platí	správné rozhodnutí	chyba 1. druhu, s rizikem a
H₀ neplatí	chyba 2. druhu, s rizikem b	správné rozhodnutí

Podobně jako v případě intervalového odhadování, existuje v soustavě (a, b , n) informační rovnováha:

při daném objemu empirické informace n (počtu měření ve výběrech) vedou vysoké nároky na úroveň a ke snížení nároků na úroveň b a obráceně; rizika chyb 1. a 2. druhu se navzájem vyvažují,
udržet obě rizika na přijatelně nízké úrovni může jenom dostatečně objemná empirická informace (rozsah dat).

Přitom je třeba mít na paměti, že rizika chyby 2. druhu tvoří vlastně celou škálu či kontinuum (tzv. silofunkce testu), z něho se obvykle jedna hodnota specifikuje (jako „vzdálenost“ alternativní hypotézy od hypotézy nulové) a pro ni se riziko chyby 2. druhu počítá.

V případě velkých výběrů se při testování hypotézy o rozdílu dvou populací může dospět k signifikantnímu výsledku i tehdy, Je-li skutečný rozdíl srovnávaných populací prakticky zanedbatelný a nezajímavý. Platí totiž, že dostatečně objemná empirická evidence dokáže odhalit libovolně „subtilní“ jev.

Hladina signifikance, na níž se nulová hypotéza zamítá, musí být stanovena předem, dříve než byla získána data tvořící výběr.

Induktivní úsudek opírající se o statistický test lze znázornit následujícím schématem:

Čajový experiment

Na večírku prohlašuje jistá dáma, že dokáže rozpoznat, zdali byl šálek čaje s mlékem připraven „technologií“ ČM (nejdříve čaj, pak mléko) anebo technologií MČ (nejdříve mléko, pak čaj). Jak se dá oprávněnost takového prohlášení ověřit?

R.A. Fisher navrhuje postup, vlastně experiment, jehož analýza umožňuje diskutovat princip statistického testu jako metody induktivního usuzování z neúplné informace.

Uvažuje se takto:

Kdyby bylo prohlášení dámy pouhým vychloubáním, tj. kdyby žádnou proklamovanou schopnost neměla, dalo by se čekat, že technologii přípravy čaje „trefí“ s pravděpodobností 1/2 a tedy s pravděpodobností 1/2 se zmýlí. Při degustaci dvou šálků čaje se dá čekat uhádnutí správné technologie přípravy obou s pravděpodobností (1/2)² = 1/4, jednoho s pravděpodobností 2(1/2)(1/2) = 1/2 a žádného s pravděpodobností (1/2)^{2 = 1/4.}

Obecně, při degustaci n šálků čaje, n = 1,2,..., popisuje chování dámy- chlubilky binomické rozdělení pravděpodobností

k: Počet správně rozpoznaných šálků z n předložených

0 1 2 3 ... n- 1 n

Pravděpodobnost rozpoznání právě k šálků z n předložených

... (1/2)ⁿ

Tak např. pro n = 5 a n = 10 dostáváme

k	P(k\|5)	k	P(k\|10)	k	P(k\|10)
0	0,031	0	0,001	6	0,205
1	0,156	1	0,010	7	0,117
2	0,312	2	0,044	8	0,044
3	0,312	3	0,117	9	0,010
4	0,156	4	0,205	10	0,001
5	0,031	5	0,246

Je tedy zřejmé, že dáma- chlubilka, podrobená zkoušce, v níž má rozpoznat n = 5 šálků, má jen malou šanci P(5|5) = 0,031 obstát bez chyby. Zkouška založená na n = 10 šálcích jí dává zcela nepatrnou šanci zařadit všech 10, případně alespoň 9 šálků, totiž Nejspíš (nejpravděpodobněji) se dá očekávat, že bude správně klasifikována přibližně polovina šálků z n předložených; výsledek pokusu je tím méně pravděpodobný, čím dále leží od středu škály veličiny k.

Statistický test považuje výchozí situaci (dáma se pouze chlubí, deklarovanou schopnost nemá) za tzv. nulovou hypotézu. Odvozená pravděpodobnostní rozdělení pak možné chování dámy kvantitativně specifikují (tj. udávají šance možných výsledků experimentu), v uvažovaném případě na stupnici počtu správně klasifikovaných šálků. Podle povahy uvažované situace jsou některé části této stupnice více a jiné méně v souladu s nulovou hypotézou; v našem případě jsou v souladu s hypotézou výsledky kolem středu stupnice a v nesouladu s ní výsledky z obou jejích krajů.

Logické schéma statistického testu je tvořeno úsudkem:

Kdyby nulová hypotéza platila, neměl by se vyskytnout málo pravděpodobný výsledek, z těch, které neodpovídají hypotéze; vyskytne-li se málo pravděpodobné (tedy vlastně skoro nemožné), lze usuzovat, že (skoro jistě) je nulová hypotéza nesprávná. V našem případě by výskyt takového nepravděpodobného výsledku z okraje stupnice vedl k závěru, že ona dáma mimořádnou schopnost správně klasifikovat čaj podle způsobu jeho přípravy opravdu má. Obráceně, Je-li výsledek pokusu (v souladu s očekáváním) vysoce pravděpodobný, hypotéza se podrží jako správná; v našem případě se tedy usoudí, že dáma má především snahu učinit se zajímavou; pokud jde o přípravu čaje, prostě se chlubí peřím, které jí nepatří.

Silofunkce statistického testu

Aby bylo možno posoudit citlivost statistického testu všestranněji, bylo by třeba najít způsob jak „vypočítat“ chování dámy v situaci, kdy opravdu jistou schopnost správné identifikace čaje podle jeho přípravy má. K tomu si však musíme náš pravděpodobnostní model trochu rozšířit.

Dejme tomu, že ona dáma dokáže správně identifikovat šálek nikoli s pravděpodobností 1/2 (odpovídající náhodnému hádání), ale s pravděpodobností p větší než 1/2. Pravděpodobnost správně klasifikovat k šálků z n předložených pak nebude dána výrazem

, ale obecnější formulí

Šance testovaného subjektu, majícího schopnost správně klasifikovat šálek s pravděpodobností p, jsou popsány- pro n = 5 a n = 10 šálků a vybrané hodnoty p = 0,7 a p = 0,9- binomickými rozděleními v následujících tabulkách:

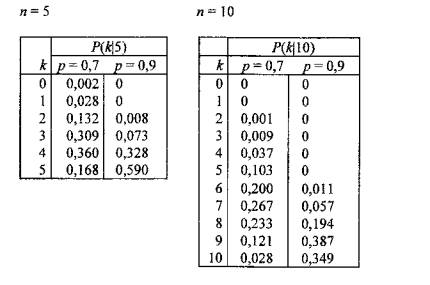
Z těchto rozdělení je zřejmé, že subjekt se schopností p = 0,7 rozpozná skoro jistě alespoň dva šálky z pěti a pět šálků z deseti předložených. Subjekt se schopností p = 0,9 pak skoro jistě alespoň tři šálky z pěti a sedm z deseti předložených. Nejpravděpodobnějšími výsledky jsou přitom k = 4 resp. k = 5 anebo k = 7 resp. k = 9 rozpoznaných šálků (z n = 5 anebo n = 10 předložených při p = 0,7 resp. p = 0,9).

Celkově se citlivost či síla statistického testu vyjadřuje tzv. silofunkcí, udávající pravděpodobnost, že schopnost subjektu bude testem rozpoznána (nulová hypotéza zamítnuta jako nesprávná) jakožto funkce P(p) skutečné schopnosti subjektu p(p = 0,5 znamená neschopnost). Samotný test je pak rozhodovací pravidlo, určující, jak posuzovat nulovou hypotézu: Bude-li správně klasifikováno alespoň k₀ šálků z n předložených, budiž deklarovaná schopnost subjektu přiznána.

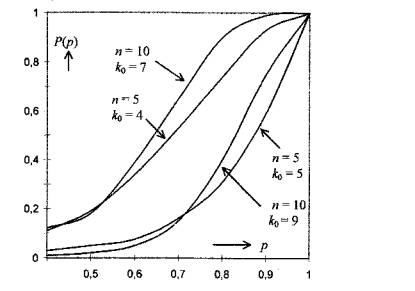
Pro n = 5 šálků byly vypracovány silofunkce testů s k₀ = 5 a k₀ = 4; pro n = 10 předložených šálků pak silofunkce testů s k₀ = 9 a k₀ = 7.

Křivky zachycující silofunkce těchto čtyř statistických testů ukazují, že při daném rozsahu empirické informace (rozsahu experimentu, tj. počtu nabídnutých šálků n) lze změnou rozhodovacího pravidla, tj. volbou k₀, silofunkci posouvat; přitom ovšem platí, že co se získá na jedné straně, na druhé se ztratí. Celkového zlepšení síly rozhodování se dosahuje pouze zvětšením rozsahu empirické informace n. Křivka silofunkce je tím lepší, čím má strmější průběh.

V čajovém experimentu nešlo ovšem jenom o čaj. Uvedená situace může posloužit jako model jiných situací, formulovatelných v pojmech zcela odlišných a vážných dokonce smrtelně.

Například tehdy, jedná-li se o hodnocení eventuálního účinku léku; úlohu dámy převezme klinik, úlohu šálku čaje dvojice „lék- placebo“, aplikovaná na pacientech, a pořadí ČM a MČ zastoupí pořadí „lék je účinnější než placebo“ a „placebo je účinnější než lék“, s tím, že obojí, lék i placebo, budou podle vhodného klíče zakódovány do barevných kapslí v nemocniční lékárně.

4 Klasifikace znalostí jako statistický problém

Princip statistického rozhodování

Klasifikace znalostí žáků je počínání, v němž není obtížné rozpoznat prvky procesu rozhodování. Tato skutečnost může být podnětem k aplikaci principů statistického rozhodování, včetně vybudování modelové situace, v jejímž rámci je taková aplikace možná. Významným motivem je přitom úsilí ono rozhodování optimalizovat, čímž je zpravidla míněna redukce „nespravedlivé“ klasifikace, kdy jsou subjekty s touž úrovní znalostí klasifikovány více nebo méně rozdílně.

Předpokládané úvahy se omezí na případ, kdy jsou znalosti hodnoceny na základě empirického měření založeného na testu typu multiple-choice.

Statistické pojetí klasifikace

Procedura klasifikace by měla uvažovat tři navzájem související struktury, jak bylo naznačeno výše:

(a) Prostor Z možných úrovní z znalostí, které přicházejí v úvahu u subjektu, jehož znalosti o daném tématu mají být klasifikovány. Předpokládá se, že tyto úrovně znalostí existují objektivně, přičemž měření examinátora jsou přístupná jenom nepřímo, přes výsledky testu (míněn je test typu multiple-choice), který zkoušený subjekt podstupuje.

Je respektována představa, že znalost tématu může mít rozličnou hloubku, například ve shodě s Bloomovou hierarchií úrovní znalostí: (1) vědění o tématu, (2) jeho pochopení, (3) analýza, (4) syntéza, (5) aplikace vědomostí o tématu, (6) řešení problémů s tématem souvisejících. Diskutovaný model neuvažuje tyto úrovně explicitně; bere je v úvahu implicitně tím, jak promítá komplexnost a obtížnost do konstrukce testových položek.

(b) Skutečná úroveň znalostí, kterou má zkoušený subjekt o uvažovaném tématu, se projevuje v jeho odpovědích v testu; jinak řečeno, tyto odpovědi jsou na úrovni znalostí závislé.

Nechť S označuje prostor možných odpovědí zkoušeného subjektu, jimiž tento může v testu reagovat; s je prvek tohoto prostoru S. Je-li použito testu typu multiple-choice, je prostorem možných odpovědí zkoušeného subjektu množina hodnot testového skóre. Tyto odpovědi jsou jediným zdrojem informace o úrovni znalostí subjektu, přístupným examinátorovi. Zdrojem tím účinnějším, čím těsněji závisí odpověď na skutečné úrovni znalosti. A protože je tato závislost uchopitelná statisticky (ve formě podmíněných pravděpodobnostních rozdělení- jak uvidíme vzápětí), je možno je také statistickými prostředky a metodami měřit.

Vyjádřeno formálněji, pravděpodobnostní rozdělení P(s|z) lze považovat za kanály, jimž proudí informace z prostoru znalostí Z do prostoru odpovědí S. V nereálném, idealizovaném případě, kdy by úroveň znalostí byla přístupná přímému pozorování a evidenci, představovala by tato podmíněná pravděpodobnostní rozdělení vzájemně jednoznačná přiřazení odpovědí znalostem; šlo by tedy o případ kanálu bez šumu.

Statistické pojetí klasifikace

Procedura klasifikace by měla uvažovat tři navzájem související struktury, jak bylo naznačeno výše:

Nechť S označuje prostor možných odpovědí zkoušeného subjektu, jimiž tento může v testu reagovat; s je prvek tohoto prostoru S. Je-li použito testu typu multiple-choice, je prostorem možných odpovědí zkoušeného subjektu množina hodnot testového skóre. Tyto odpovědi jsou jediným zdrojem informace o úrovni znalostí subjektu, přístupným examinátorovi. Zdrojem tím účinnějším, čím těsněji závisí odpověď na skutečné úrovni znalosti. A protože je tato závislost uchopitelná statisticky (ve formě podmíněných pravděpodobnostních rozdělení - jak uvidíme vzápětí), je možno je také statistickými prostředky a metodami měřit.

(c) Klasifikační procedura tak představuje soustavu rozhodovacích pravidel, přiřazujících každé odpovědi s z S právě jediný klasifikační stupeň (klasifikační kategorii) r klasifikační škály R. Znamená to, že klasifikační procedurou je zaváděn vztah mezi empirickou (examinační) evidencí S a klasifikací (rozhodnutím) R.

V pojmech experimentální psychologie to znamená, že prostor rozhodnutí R, stejně jako pravidla klasifikace jsou kontrolovány examinátorem, zatímco prostor znalostí Z a prostor odpovědí S jsou kontrolovány zkoušeným subjektem.

Klasifikační procedura tak představuje exhaustivní (vyčerpávající) a jednoznačný rozklad prostoru odpovědí S do konečné množiny m vzájemně se nepřekrývajících podmnožin s₁, s₂, ..., s_m tak, aby byl zkoušený subjekt klasifikován stupněm r_i, jestliže jeho odpověď byla prvkem podmnožiny s_i, i = 1, 2, ..., m.

Při hledání optimální klasifikační procedury lze aplikovat představy známé z Neymanovy a Pearsonovy koncepce testování statistických hypotéz.

Pro daná klasifikační pravidla se zavádí soustava tzv. operačních charakteristik klasifikace, což je m funkcí i = 1,

2, ...,m, každá z nich odpovídající právě jednomu z m klasifikačních stupňů r_i. Argumentem každé takové funkce je skutečná úroveň znalostí z; svých hodnot nabývá funkce v oboru jako podmíněná pravděpodobnost, že zkoušený subjekt bude klasifikován stupněm r_i, tj., že jeho odpověď bude prvkem podmnožiny odpovědí s_i. Pro danou hodnotu z tvoří m odpovídajících hodnot P(r_i|z) (podmíněné) pravděpodobnostní rozdělení, protože

S klasifikací je spojen problém její spolehlivosti. Zdrojem nespolehlivosti je přitom

(1) diskretizace, event. zhrubení spojité, případně detailněji vzorované škály odpovědí S do systému podmnožin {s₁, s₂, ..., s_m} a

(2) neurčitost existující ve vztahu mezi úrovní znalostí z a odpovědí s, což způsobuje, že v množině subjektů s touž úrovní znalostí z nebudou všichni klasifikováni stejně; tak se vynořuje otázka „klasifikační nespravedlnost“ co nejvíce redukovat.

Binomické rozdělení odpovědí

Takto chápaný model rozhodování může být hlouběji formalizován v případě, kdy se měření znalostí opírá o test typu multiple-choice a kdy se odpověď zkoušeného subjektu umisťuje na stupnici testového skóre.

Aktuální znalost subjektu o předmětu zkoušky představuje v modelu pravděpodobnost p jeho nesprávné odpovědi. Nízké hodnoty p (blízké nule, případně blízké „statistické nule“, má-li v testu své místo možné dosažení správného řešení úlohy náhodným uhádnutím) odpovídají lepší znalosti, vyšší hodnoty p (blízké jedné) odpovídají špatné znalosti.

Předpokládá se, že test je tvořen souborem n vzájemně nezávislých položek (úloh) dané úrovně obtížnosti. S každou testovou úlohou se zkoušenému předkládá q alternativ odpovědí (různých řešení), z nichž právě jediná je správná a zbylých q- 1 nabídek plní funkci distraktorů.

Odpovědí subjektu v testu jako souboru n položek je počet k (0 £ k £ n) nesprávných odpovědí (k nesprávně řešených úloh) z n úloh předložených- tj. hrubé skóre nesprávných odpovědí. Znamená to, že podmíněné pravděpodobnosti odpovědí subjektu, kdy podmínkou je úroveň znalostí, nabývá formy binomického rozdělení

(3.6.1)

Klasifikační pravidlo rozkládá množinu {0,1, ..., n} možných odpovědí zkoušeného subjektu do m disjunktních podmnožin tak, aby každý z m klasifikačních stupňů byl přiřazován právě jediné z těchto podmnožin (vzájemně jednoznačné zobrazení). To pak umožňuje odvodit příslušný soubor m operačních charakteristik klasifikace.

Operační charakteristiky klasifikace

Soustava operačních charakteristik klasifikace je ovlivňována nejen rozsahem testu n, počtem používaných klasifikačních stupňů m, ale také tím, jakým způsobem byl proveden rozklad škály skóre chybných odpovědí do soustavy {s₁, s₂, ..., s_m}. Operační charakteristiky jsou tak definovány vzorci

(3.6.2)

Testovému výsledku s₁ (malý počet chyb) je zřejmě přiřazován nejlepší klasifikační stupeň, zatímco testový výsledek s_m (velký počet chyb) se oceňuje nejhorším klasifikačním stupněm m.

Obr.3.2 až 3.10 zachycují soustavy operačních charakteristik v situacích, kdy jsou prověřovány znalosti pomocí testu s volbou z nabídnutých odpovědí (multiple-choice test) s n = 10, 20 či 30 položkami a m = 2, 3, případně 4 kvalifikačními stupni. Klasifikační pravidla jsou definována v popisu každého grafu.

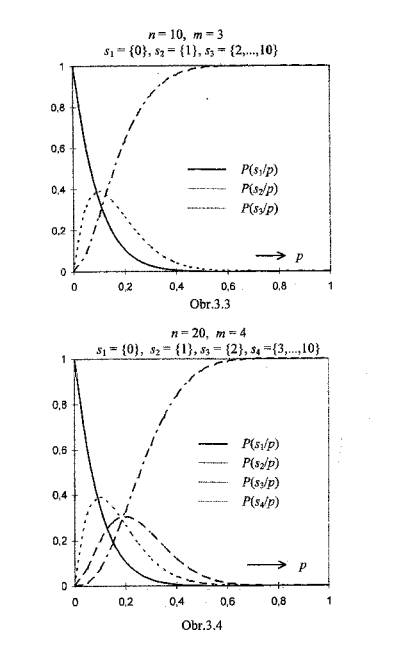
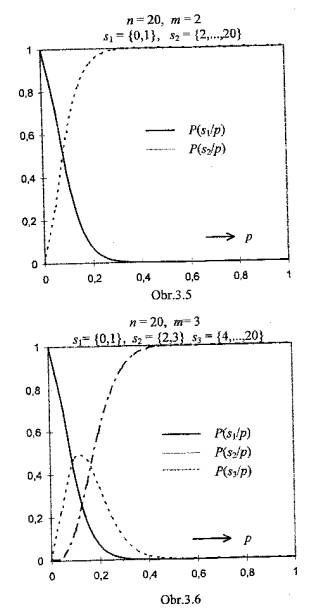
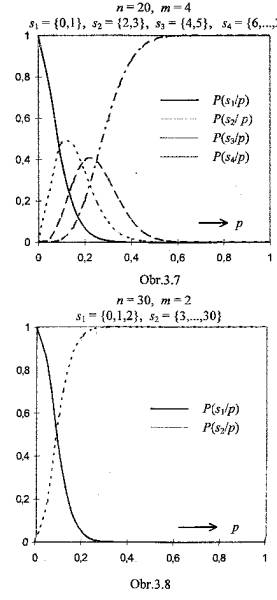
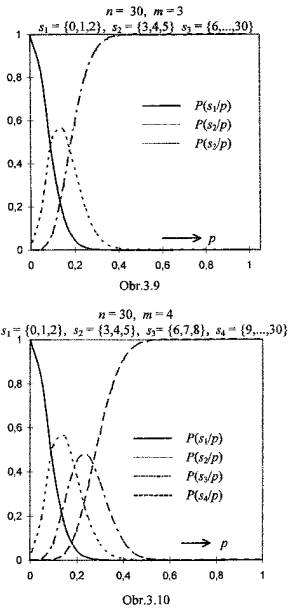
Pro každou hodnotu p(na vodorovné ose) udávají křivky operačních charakteristik, jaký podíl subjektů (jejichž znalostem odpovídá pravděpodobnost chybné odpovědi p) bude klasifikován tím kterým stupněm. To, že jedinci s touž úrovní znalostí mohou být klasifikováni rozdílně, je nepochybně nedostatkem procesu klasifikace- průvodním znakem jeho nedokonalosti, která může být interpretována jako projev nespravedlnosti hodnocení a tedy křivdy.

Vliv rozsahu testu n na nespravedlnost klasifikace je zřejmý: při daném počtu klasifikačních stupňů m jsou v případě rozsáhlejšího testu křivky operačních charakteristik strmější, díky čemuž se jednotlivé klasifikační stupně váží na znalosti specifičtěji.

Závislost operačních charakteristik a tím také nejednoznačnosti klasifikace na počtu použitých klasifikačních stupňů m není tak jednoznačně interpretovatelná. Hodnocení a porovnání musí brát v úvahu, že klasifikační stupně jsou úrovněmi ordinálního znaku, a že „vzdálenost“ mezi stupni „1“ a „2“ ve dvoubodové škále (m = 2) je podstatnější nežli „vzdálenost“ mezi stupni „1“ a „2“ ve škále čtyřbodové (m = 4).

Distance jako kritérium neurčitosti klasifikace

Spíše než nominální má klasifikační škála povahu ordinální. Je proto vhodnou statistikou neurčitosti rozdělení P(r_i|p), i = 1, 2, ..., m, distance, schopná vzít v úvahu uspořádání stupňů klasifikační škály.

Distanci zavádíme vztahem

. (3.6.3)

Funkce (3.6.3) nabývá svého minima (v případě, kdy

P(r_i|p) = 1 pro některé i a nula pro i ostatní) a svého maxima

d(p) = (m- 1)/4 (v případě, kdy a ostatní pravděpodobnosti jsou rovny nule).

Jako míra spolehlivosti klasifikace může proto sloužit statistika odvozená ze (3.6.3) standardizací, totiž

, (3.6.4)

jejíž minimální hodnota 0 znamená nejnižší a maximální hodnota 1 nejvyšší možnou spolehlivost klasifikace.

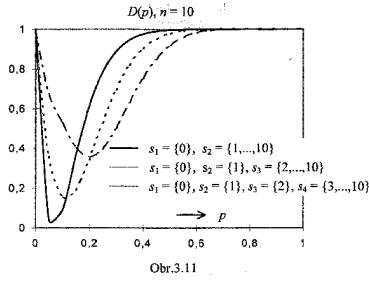
Křivky spolehlivosti klasifikace (3.6.4) jsou zachyceny pro uvažované strategie na Obr. 3.11- 3.13.

5 Testy pro výběry velkého rozsahu

V předcházejícím odstavci byla zmínka o tzv. asymptotickém rozdělení náhodné veličiny, opírajícím se o centrální limitní věty. To se také označuje jako zákon velkých čísel a umožňuje v mnoha případech zjednodušení řešené úlohy s využitím normálního rozdělení. V politologickém, případně sociálním výzkumu, existují početné aplikace známé jako úlohy o procentech.

Příklad. Ve velkém městě odebírá 20% domácností časopis J. Po zdražení, k němuž došlo, se dá očekávat pokles počtu předplatitelů. Veličina P (= podíl předplatitelů v městské populaci,má přibližně (díky velkému počtu obyvatel n) normální rozdělení pravděpodobností s parametry: střední hodnotou m = 0, 20 a rozptylem .

Ve vzorku n = 100 náhodně vybraných obyvatel města, (po zdražení) dotázaných, zdali jejich domácnost odebírá časopis J (jednotkou šetření je domácnost, ne jedinec), odpovědělo pozitivně 16. Má se ověřit hypotéza, že zdražení časopisu nemělo vliv na jeho subskripci.

Za platnosti nulové hypotézy má standardizovaný podíl respondentů ve výběru

(n je rozsah výběru) standardizované normální rozdělení N(0, 1). Jde tedy o to, zda-li je výsledek 16 ze 100 dosti pravděpodobný anebo příliš nepravděpodobný- vzhledem k platnosti nulové hypotézy.

Dosadíme-li za P = 16/100 = 0,16 a n = 100, zjistíme, že pokles na 16 a méně procent se dá za platnosti nulové hypotézy (jako projev pouhého náhodného kolísání ve výběru rozsahu n respondentů) očekávat s pravděpodobností

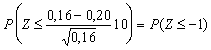kde Z je náhodná veličina s rozdělením N(0, 1). Z tabulky standardizovaného normálního rozdělení zjistíme, že hledaná pravděpodobnost se rovná 0,159 (viz Obr. 3.14). Nalezený výsledek je pořád ještě za platnosti H₀ dostatečně vysoce očekávaný- vliv zdražení na subskripci nebyl prokázán.

Kritickým oborem pro test uvažované hypotézy, podle níž zdražení časopisu J neovlivní zájem předplatitelů, je interval Z £ -1,645 (protože a tato oblast nejméně svědčí ve prospěch H₀ a nejvíce ve prospěch její alternativy H:-zdražením předplatitelský zájem klesá?.

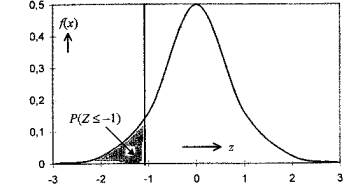
Obr.3.14

Příklad. Politická strana získala v parlamentních volbách 53% hlasů (volily milióny voličů). Po půl roce, při průzkumu aktuálních volebních preferencí, prohlásilo pouze 96, tj. 48% z 200 respondentů, že by v případě nových voleb stranu volilo. Otázka zní, má-li být nález interpretován jako důkaz pokleslé prestiže strany anebo jako pouhý projev náhodného kolísání v důsledku omezenosti rozsahu výběru.

Podíl příznivců uvažované politické strany ve výběru rozsahu n je náhodná veličina P s přibližně normálním rozdělením s parametry m = 0,53 a s² = 0,53× 0,47/n = 0,2491/200 = 0,0012455, a tedy veličina (P- 0,53)/0,035; , má standardizované normální rozdělení N(0, 1).

Nulová hypotéza H₀ konstatuje, že pokles zájmu voličů ve výběru je pouze nahodilý jev. Kritickým oborem testu takové hypotézy je zřejmě interval nízkých hodnot P, odvoditelný z požadavku, aby (P- 0,53)/0,035 <-1,645 (viz tabulka standardizovaného normálního rozdělení a předcházející příklad). Test s tímto kritickým oborem má signifikanci 0,05. Po úpravě je vymezen nerovností

P < 0,53- 1,645 × 0,035 , tj.

P < 0,4725 .

Teprve pokles (ve výběru rozsahu n = 200) pod 47% by dokazoval se spolehlivostí 0,95, že strana ztrácí příznivce. Pokles popularity na 48% je ještě vysvětlitelný náhodným kolísáním ukazatele ve výběru, jak dokazuje výpočet

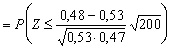
(kde Z má rozdělení N(0, 1))

= P(Z ? -1,43)

= 0,08 > 0,05 .

Pozn. U obou posledních příkladů šlo o jednostranné testy.

Příklad. Má se zjistit, vidí-li neprovdané ženy svou budoucnost stejně růžově jako ženy vdané. Ve dvou souborech srovnatelných co do věku, sociálního postavení, typu bydliště a dalších relevantních znaků životního stylu, žádala anketní otázka, aby se respondentka vyslovila pro spíše optimistické anebo spíše pesimistické vidění budoucnosti, tj. pro důvěru či nedůvěru v budoucnost.

Výsledky šetření daly v uvedené položce výsledky

vzorek souboru

důvěru v budoucnost

vyslovil podíl

vdané (V)

n_V = 642

p_V = 0,631, tj. 63,1%

neprovdané (N)

n_N = 985

p_N = 0,590, tj. 59,05

Má se posoudit, zdali má rodinný stav vliv na způsob vidění budoucnosti.

Jde o porovnání dvou relativních četností- ve dvou populacích. Nulová hypotéza předpokládá, že v referenčních populacích, z nichž byly naše dva výběry vzaty, je podíl optimistických žen stejný.

Abychom zkonstruovali kritický obor testu, vyjdeme z faktu, že při dostatečně velkých výběrech n_V a n_N má veličina

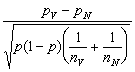, (3.7.1)

kde

(3.7.2)

přibližně standardizované normální rozdělení N(0, 1).

Kritický obor testu (tentokrát dvoustranný) má tvar (jak ukazuje Obr.3.14 a tabulka standardizovaného normálního rozdělení), při hladině signifikance 0,95,

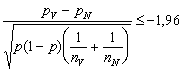
a 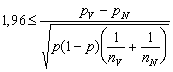. (3.7.3)

Dosazením za p_V, p_N, n_V a n_N se přesvědčíme, padnou-li data do kritického oboru testu či nikoli. Dostáváme tak

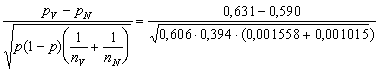
Vypočítaná hodnota leží mimo kritický obor dvoustranného testu. Není tedy prokázáno, že by rodinný stav ovlivňoval důvěru v budoucnost v uvažované referenční populaci žen (vymezené věkem a dalšími faktory).

Pozn. Při jednostranném testu by vypočítaný výsledek ležel už nad hranicí statistické signifikance.

Příklad. Globální údaje o sledovanosti televize uvádějí, že v průměru se dívá občan (včetně dětí školního věku) na televizi 6,2 hodin denně.

Náhodný vzorek n = 1017 starších občanů poskytl data, jejichž průměr je hodin denně, se směrodatnou odchylkou .

Má se posoudit, zdali se sledovanost televize staršími občany liší od její sledovanosti v obecné populaci. Nulová hypotéza H₀ tvrdí, že sledovanost televize na věku diváka nezávisí.

Označme X počet hodin, které občan denně stráví sledováním televize. Má-liX alespoň přibližně normální rozdělení, má veličina

(za platnosti H₀) přibližně rozdělení N(0, 1). Kritický obor testu (dvoustranný, na úrovni signifikance 0,10) je vymezen intervaly

tj.

neboli

(viz odhad)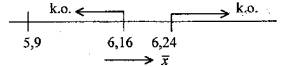

Výsledek testu je tedy signifikantní; starší lidé sledují TV méně často než odpovídá standardu obecné populace.

Archimédes a syrakusští zlatníci

O řeckém učenci Archimédovi ze sicilského města Syrakus se vypráví příběh, podle něhož aplikoval svůj právě (ve 3.stol. př. Kr.) objevený princip, známý dnes ze školských učebnic fyziky jako Archimédův zákon („Těleso do kapaliny ponořené je nadlehčováno silou, která se rovná váze kapaliny tělesem vytlačené“), aby odhalil nepoctivost městských zlatníků. Podnět k řešení úlohy dal údajně syrakuský vládce (tyrannos) Hiero, který pojal podezření, že zlatníci „na zlatě ošidili“ korunu, jejíž zhotovení jim zadal. Objevený zákon umožnil Archimédovi určovat měrnou hmotnost těles jakkoli nepravidelných tvarů, tedy i koruny (dnes je to běžná součást fyzikálních cvičení).

V následujícím textu se pokusíme naznačit, jak by asi Archimédes řešil úlohu Hieronem mu zadanou, kdyby byl obeznámen s metodou statistického testování.

Označme jako X měrnou hmotnost přezkušované koruny, zhotovené podezíranými zlatníky. Zadání znělo: z čistého zlata. Archimédova metoda stanovení měrné hmotnosti má ovšem- jako každá jiná- chybu měření, jejíž existence se částečně překonává opakováním měření. Měrná hmotnost čistého zlata (stanovená a ověřená rozsáhlou zkušeností) je rovna 19,3 g × cm^-3. To umožňuje formulovat nulovou hypotézu

a k ní alternativu

(předpokládá se, že podle zvyklostí podvodníků oné doby by ukradené zlato bylo nahrazováno lacinějším (a lehčím) stříbrem, jehož měrná hmotnost se rovná 10,5 g × cm^-3. Povaha chyb měření způsobuje, že veličina X má za platnosti H₀ rozdělení přibližně normální- se střední hodnotou m₀ a rozptylem, jejž stanovuje zkušenost na .

Řekněme, že Archimédes opakoval stanovení měrné hmotnosti koruny, dodané syrakuskými zlatníky n = 4krát.

Náhodná veličina má za platnosti H₀ normální rozdělení se střední hodnotou m = 19,3 a směrodatnou odchylkou . Standardizovaná veličina

má tedy rozdělení N(0, 1).

Kritický obor testu tvoří (tj. vyvolávají podezření, že „zlatá“ koruna obsahuje nějaké vmíchané stříbro) nízké hodnoty z. Hranice kritického oboru testu se určí z požadavku, aby poctiví zlatníci (jsou-li, tj. platí-li H₀) byli (neprávem) pověšeni za krádež královského zlata jenom s nepatrným rizikem, řekněme 0,01 (1:100), tj. aby

kde z_0,01 je 1%-ní kvantil standardizovaného normálního rozdělení. Zapsáno jinak,

a protože v tabulce kvantilů rozdělení N(0, 1) máme

z_0,01=-2,33 ,

dostáváme konečně pro kritický obor tohoto (jednostranného) testu interval

, tj. .

Měl by tedy Archimédes, kdyby byl přijal za svůj princip statistického testování, dát svému tyranu Hieronovi radu, aby považoval zlatníky za provinilé, jestliže průměr ze 4 opakovaných zjišťování měrné hmotnosti královské koruny klesne pod hodnotu 18,95 g × cm^-3.

Zajímavou úlohou by teď bylo- spočítat, jak závisí výsledek aplikace této Archimédovy rady na velikosti případného provinění zlatníků, tj. na tom, kolik zlata zcizili a nahradili lacinějším stříbrem: Vyjít se přitom dá z předpokladu, že zlatníci odvedli Hieronovi korunu v té hmotnosti (váze), kterou s ním předem dohodli, a že zlato je mnohonásobně dražší než stříbro (nejméně dvakrát, protože jinak by úloha, vzhledem k poměru měřených hmotností obou kovů, ztratila smysl.

Hledaná závislost se dá měřit pravděpodobností, že měření padnou do kritického oboru, v situaci, kdy zlatníci zhotovili korunu z c dílů zlata a 1- c dílů stříbra, což je

, kde

neboli

Na levé straně nerovnosti je veličina Z s rozdělením N(0, 1), takže je hledaná pravděpodobnost rovna

Konstanta c je mírou provinění zlatníků; c = 1 (samé zlato) udává stav jejich poctivosti. Následující tabulka popisuje hledanou závislost pravděpodobnosti odhalení přestupku na jeho závažnosti, tj., vlastně sílu (citlivost) testu

c	56,33- 58,67c	P(Z < 56,33- 58,67c
1	-2,34	0,01 = signifikance, riziko pověšení nevinných
0,99	-1,75	0,04
0,98	-1,17	0,12
0,97	-0,58	0,38
0,96	0,01	0,50
0,95	0,59	0,72
0,94	1,18	0,88
0,93	1,77	0,96
0,92	2,35	0,99
0,91	2,94	1

Je tedy zřejmé , že nahradí-li zlatníci více než 10% zlata stříbrem, riskují šibenici naprosto jistě. Zmíněná závislost je zřejmá také z grafu

6 Studentův t-test

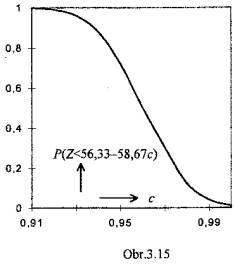
Při řešení úloh o statistickém chování náhodných veličin alespoň přibližně normálně rozdělených, u nichž však není k dispozici spolehlivý apriorní odhad jejich rozptylů, se využívá t-rozdělení podle Studenta. Neznámý rozptyl s² se přitom odhaduje pomocí výběrového rozptylu s². V úlohách tohoto typu se testují hypotézy o střední hodnotě sledované veličiny v jedné populaci (tzv. t-test pro jeden výběr) a hypotézy o rovnosti středních hodnot ve dvou různých experimentálních situacích (tzv. t-test pro dva výběry). V posledně uvedeném případě pak může být informace obsažena v nezávislých datech (tzv. nepárový t-test) anebo v datech tvořících dvojice (tzv. párový t-test).

Při řešení úloh se využívá dostupných tabulek percentilů (kvantilů) Studentova t-rozdělení.

Některé úlohy tohoto typu teď uvedeme.

Příklad. Předmětem studia je spokojenost žen s jejich rodinným životem. Veličina vyjadřující spokojenost je měřena na škále, v níž nízké hodnoty znamenají malou a vysoké hodnoty velkou spokojenost. Má se testovat, zdali je rozdíl ve statistickém chování sledované veličiny v případě žen bezdětných a žen s dětmi. Tímto chováním rozumíme posun na škále spokojenosti. Nulová hypotéza H₀ předpokládá, že rozdíl v chování není.

Jedná o test pro dva výběry: B (bezdětné) a D (s dětmi), v nepárovém uspořádání.

Údaje o počtu žen, které spolupracovaly, průměrných hodnotách skóre a směrodatných odchylkách jsou

	B	D
Rozsah výběru
Průměr
Směrodatná odchylka

Oprávněnost nulové hypotézy se prověřuje testovým kritériem

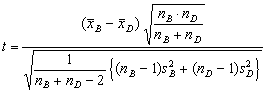(3.9.1)

majícím (za platnosti H₀) t-rozdělení o n_B + n_D- 2 stupních volnosti. Dvoustranný test na hladině signifikance 0,05 má kritický obor vymezen nerovnostmi (jak zjistíme z tabulek kvantilů t-rozdělení) při n_B + n_D- 2 = 78 + 93- 2 = 169 stupních volnosti

t <-1,96 a 1,96 < t .

Po dosazení do (3.9.1) dostáváme

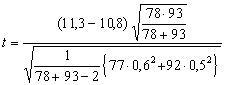
Testy tedy končí statisticky signifikantním výsledkem: bezdětné ženy jsou s rodinným životem spokojenější nežli ženy s dětmi.

Použité výběry jsou dostatečně rozsáhlé, aby bylo oprávněné použití normální aproximace (viz předchozí příklady).

Rozdíl průměrů má (za platnosti nulové hypotézy) přibližně normální rozdělení s parametry m = 0 a

takže ( je standardizovaná náhodná veličina s rozdělením N(0, 1). Příslušný dvoustranný test provedený na hladině významnosti 0,05 má pak kritický obor

(t-rozdělení pro stovky stupňů volnosti je prakticky shodné se standardizovaným rozdělením normálním).

Po dosazení dostáváme

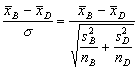
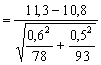
Vypočítaná hodnota leží hluboko v kritickém oboru testu- a potvrzuje tak platnost závěru opírajícího se o t-test.

Je-li možno při srovnání chování veličiny ve dvojích podmínkách měření opakovat, případně uspořádat jedince do párů tak, aby si byli oba členové páru co nejvíce podobní v dalších ohledech, které mohou mít na sledovanou veličinu vliv, používá se při analýze vlivu podmínek párového t-testu. Párový způsob uspořádání pokusu snižuje variabilitu pozorování a umožňuje tak odhalit eventuálně existující vliv účinněji, citlivěji.

Příklad. Má se posoudit, dokáže-li jistý, cíleně natočený film ovlivnit předsudky lidí (z určité referenční populace) vůči společenským minoritám. Dotazníková škála dává vyšší hodnoty pro vyšší úrovně předsudků. Vyšetřeno bylo n = 15 osob.

Primární data tvoří páry typu: pretest- posttest (před shlédnutím filmu a po něm); z nich se vypočítají diference d_i, i = 1, ..., n, průměrná diference

a rozptyl diferencí

Testovým kritériem pro test nulové hypotézy o neúčinnosti filmu je charakteristika

, (3.9.2)

která má- za platnosti nulové hypotézy- t-rozdělení o n- 1 stupních volnosti.

Kritickým oborem pro jednostranný test na hladině významnosti 0,05 je interval (vysoké hodnoty a tedy i t zpochybňují oprávněnost hypotézy) t_0,95(n- 1) < t, kde t_0,95(n- 1) je 95%-ní kvantil t-rozdělení o n- 1 stupních volnosti. Z tabulek t-rozdělení tak najdeme, že t_0,95 (14) = 1,761 .

Data shrnuje tabulka

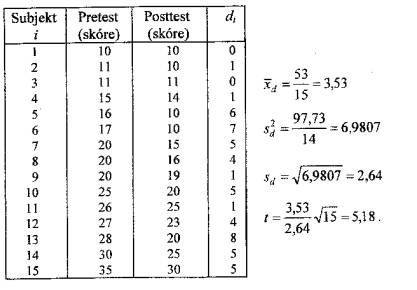
Hodnota testového kritéria leží v kritickém oboru testu; usuzujeme proto, že shlédnutí filmu dokáže snížit úroveň nesnášenlivosti (předsudků, intolerance) vůči minoritám.

7 Neparametrické testy

Dosud uváděné testy předpokládaly, že sledovaná veličina, jejíž chování test posuzuje, splňuje některé poměrně náročné podmínky: normalitu pravděpodobnostního rozdělení, znalost jeho rozptylu, případně rovnost rozptylů (tzv. homoskedastičnost) v případě testů pro dva výběry.

Neznalost rozptylů překonává Studentův t-test. Neznalost rozdělení testované veličiny není na překážku tzv. neparametrickým testům. Aplikaci některých z nich budeme demonstrovat.

Znaménkový test

Případ, kdy úloha vede k získávání párových dat, je analogií situace v tzv. čajovém experimentu, diskutovaném dříve. Příslušný test nese název test znaménkový. V podstatě jde o to, že za platnosti nulové hypotézy (žádná ESP schopnost, žádný rozdíl v účinnosti srovnávaných dvojích podmínek) by se znaménka diferencí měla chovat jako opakovaně házená mince: počty kladných a záporných výsledků by měly být přibližně stejné- právě tak jako počty hlav a lvů na házené minci.

Kritickým oborem testu jsou nečekaně vysoké anebo nečekaně nízké počty kladných či záporných diferencí. Hranice kritického oboru testu se stanoví z tabulek binomického rozdělení (s parametry n, p = 1/2).

AplikuJe-li se znaménkový test na poslední příklad předchozího odstavce 3.9, snadno se zjistí, že 13 kladných diferencí z n = 15 pokusů je- za platnosti nulové hypotézy- jev téměř nemožný. Protože nastal, soudíme, že hypotéza je nepravdivá- což je v souladu se závěrem párového t-testu podle Studenta.

U-test

Případné nesplnění požadavku, aby byla sledovaná veličina normálně rozdělena, překonávají neparametrické testy například tím, že nahrazují pozorování (primární data) jejich pořadími a kritický obor testu konstruují za pomoci kombinatorických metod. Samotný název „neparametrický“ test je odvozován z faktu, že nulová hypotéza není tvrzením o parametru pravděpodobnostního rozdělení, ale o nějaké obecnější vlastnosti tohoto rozdělení.

U-test Manna a Whitneyho řeší podobnou úlohu jako t-test pro dva nezávislé výběry: nulová hypotéza tvrdí, že pravděpodobnostní rozdělení hledané veličiny ve dvojích, rozdílných, experimentálních podmínkách, nejsou vůči sobě posunuta a jejich středy zaujímají tedy stejnou polohu.

Empirickou informaci použitelnou pro ověření platnosti nulové hypotézy obsahují dva výběry; daty jsou hodnoty sledované veličiny.

Testové kritérium se počítá takto:

Data obou výběrů se smíchají
Data ve smíchaném souboru se nahradí jejich pořadími
Počítá se hodnota testového kritéria U: pro každé pozorování z prvého výběru se zjistí, kolik pozorování ve druhém výběru mu předchází (tzv. počet inverzí); zjištěné hodnoty se sečtou a označí jako U₁. Totéž se provede při záměně úloh výběru; výsledek se označí symbolem U₂.

Funkce testu se zakládá na následující úvaze:

Kdyby platila nulová hypotéza H₀ (v obou srovnávaných populacích, z nichž byly vzaty naše vzorky, jsou úrovně sledovaného znaku rozděleny stejně), neměla by se pořadí, která zaujímají data z prvního a druhého výběru ve smíchaném výběru, systematicky odlišovat. Jinak řečeno, nízká a vysoká pořadí by měla být zastoupena v obou výběrech přibližně rovnoměrně. Testovým kritériem je počet inverzí U₁- tj. počet dvojic pozorování (pořadí), kdy je pořadí v prvním výběru vyšší nežli pořadí ve druhém výběru; takových dvojic pozorování je třeba přezkoušet n₁ × n₂, kde n₁a n₂ jsou rozsahy prvního a druhého výběru. Kritérium U₁ se může v krajním případě rovnat n₁n₂ (jestliže i nejnižší pořadové číslo v prvním výběru je větší než nejvyšší pořadové číslo ve druhém výběru), případně 0 (jestliže obráceně i to nejvyšší pořadí v prvním výběru je nižší nežli nejnižší pořadí ve výběru druhém). Stejným způsobem- po záměně rolí obou výběrů- se může vypočítat veličina U₂. Přitom platí vztah (což může sloužit jako kontrola výpočtu) U₁ + U₂ = n₁n₂.

Při větších rozsazích výběrů n₁ a n₂ je pohodlnější počítat U₁ a U₂ nepřímo, s využitím jejich vztahů k součtům pořadí R₁ a R₂ v prvním a v druhém výběru.

Platí totiž

(3.10.1)

Jako kontrola součtu pořadí může přitom sloužit vztah

O eventuální statistické významnosti testu rozhoduje srovnání vyšší z obou vypočítaných hodnot v (3.10.1) s kritickou hodnotou v tabulce (závisející na n₁, n₂, zvolené hladině signifikance aa na tom, zdali má být H₀ testována proti jednostranné nebo oboustranné alternativě).

Příklad. Výkon 18 gymnastek byl ohodnocen stanovením jejich pořadí od nejlepší (pořadí 1) po nejslabší (pořadí 18). V této skupině bylo n₁ = 11 žákyň trenérky A a n₂ = 7 žákyň trenérky B. Na základě výsledků (pořadí) shrnutých v tabulce se má posoudit nulová hypotéza H₀:-účinnost výukových metod obou trenérek se neliší?.

Přitom se předpokládá, že rozřazení gymnastek do obou skupin nijak nesouvisí s jejich případným talentem či dispozicí pro cvičení uvažovaného typu.

Trenérka:

, anebo

(kontrola)

, anebo

(kontrola)

V tabulce U-rozdělení najdeme- pro výběry rozsahu 7 a 11, a = 0,05 a oboustranný test- kritickou hodnotu U_0,05 (7, 11) = 61. Za platnosti H₀ nabývají hodnoty testového kritéria U svých hodnot v intervalu á 0, 77ñ, se středem n₁n₂/2 = 38,5. Statisticky signifikantní jsou hodnoty U větší nebo rovné 61 anebo menší nebo rovné 77- 61 = 16. Výsledek testu je tedy nesignifikantní: hodnocení výkonů gymnastek neprokázalo rozdíl v účinnosti metod obou trenérek.

Jsou-li oba výběry velké (n₁, n₂ > 20), má kritérium U přibližně normální rozdělení s parametry

, , (3.10.2)

takže lze test založit na standardizované veličině

V situacích, kdy jsou data uspořádána ve formě četnostních tabulek, je řada typů úloh řešitelná s využitím charakteristiky c²-chí kvadrát (1.8.10). Zpravidla jde o nominální znaky, případně znaky ordinální nebo metrické, které byly druhotně do podoby znaků nominálních kategorizovány. -

První z příkladů patří mezi tzv. testy dobré shody, druhý je testem homogenity.

Příklad. V dotazníku šetřícím veřejný názor o tom, které z oblastí by měla být věnována prvořadá pozornost, se n = 500 respondentů vyslovilo v souladu s daty v tabulce

i	Oblast preference	Počet respondentů, kteří zařadili tuto oblast jako nejvíce hodnou pozornosti n_i
1	Znečištění ovzduší, vody, půdy	40
2	Zajištění zdrojů energie	97
3	Odstranění bídy	31
4	Dostupnost lékařské péče	85
5	Zahraniční politika	53
6	Zabezpečení ochrany státu	71

	Nevrácené dotazníky	123
	å	500

Vhodným statistickým testem se má rozhodnout, Je-li některá z uvedených oblastí považována za naléhavější než jiné. Jinak řečeno, má se ověřit platnost nulové hypotézy, že všechny uvedené problémy považuje populace, z níž byl vzorek n = 500 respondentů vybrán, za stejně významné.

Úloha může být řešena jako test hypotézy, že rozdělení preferencí do oněch 6 oblastí je rovnoměrné, totiž rovné

. Příhodným je test dobré shody, založený na kritériu chí-kvadrát, kdy jsou porovnávány empiricky pozorované četnosti s teoretickými, jak je postuluje nulová hypotéza.

Testové kritérium má tvar

(3.10.3)

Kritérium má přibližně c²-rozdělení o k- 1 stupních volnosti, kde k je počet stavů náhodné veličiny. V naší úloze tedy

protože

Z tabulek percentilů c²-rozdělení zjistíme, že vypočítaná hodnota leží hluboko v kritickém oboru testu. Kritický obor je přitom tvořen relativně vysokými hodnotami, v případě k- 1 = 5 stupňů volnosti hodnotami vyššími než 11,1,

c² > 11,1.

Příklad. Byl prováděn průzkum s cílem zjistit, zdali je názor rodičů na společný život mladých lidí (mimo manželství) ovlivněn věkem jejich nejmladšího dítěte. Získaná data shrnuje tabulka

Věk nejmladšího dítěte	Názor rodičů schvalují neschvalují				å
Nad 26 let	10	(30)	40	(20)		50
18- 25 let	50	(36)	10	(24)		60
Pod 18 let	60	(54)	30	(36)		90
?	120		80			200

Úlohu lze řešit jako test homogenity c², kdy se testuje nulová hypotéza, že ve všech třech subpopulacích (těm odpovídají řádky tabulky) je pravděpodobnost souhlasného názoru táž.

Testové kritérium c² je dáno formulí

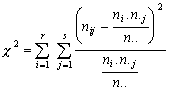(3.10.4)

kde r a s jsou počty řádků a sloupců tabulky, a má přibližně c²-rozdělení o (r- 1)(s- 1) stupních volnosti. Údaje v tabulce jsou empirické četnosti n_ij a v závorce teoretické četnosti očekávané za platnosti H₀. V našem případě tak máme speciálně r = 3, s = 2 a

Z tabulky c²-rozdělení (pro 2 stupně volnosti a signifikanci 0,05) zjistíme, že kritický obor testu tvoří hodnoty vyšší než 5,99. Výsledek testu je tedy statisticky signifikantní- data prokázala, že názor rodičů na mimomanželské soužití mladých lidí závisí na věku jejich nejmladšího dítěte.

8 Korelace a regrese

Má-li dvojice náhodných veličin X, Y alespoň přibližně dvourozměrné normální rozdělení, je její pravděpodobnostní hustota určována jednak středními hodnotami E(X), E(Y) a rozptyly D(X), D(Y) veličin X a Y, ale také jejich korelačním koeficientem r_XY, 0 £ r_XY£ 1; ten vyjadřuje těsnost závislosti X a Y.

Náhodný výběr n párů pozorování či měření (x₁, y₁), ..., (x_n, y_n) umožňuje odhadovat parametry uvedeného teoretického modelu pomocí výběrových průměrů a , výběrových rozptylů a a pomocí výběrového korelačního koeficientu

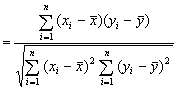(3.11.1)

Výběrový (Pearsonův) korelační koeficient (3.11.1) měří stupeň závislosti veličin X a Y na škále od-1 do 1, přičemž hodnoty blízké nule vypovídají o tom, že sledované veličiny X resp. Y nenesou prakticky žádnou informaci o Y resp. X, zatímco hodnoty korelačního koeficientu blízké-1 či 1 svědčí o blízkém lineárním vztahu X a Y. Záporná korelace přitom znamená, že na měřených objektech jsou nízké hodnoty veličiny X doprovázeny spíše vysokými hodnotami veličiny Y (a obráceně); kladná korelace dokazuje, že na objektech s vysokými hodnotami jedné veličiny lze očekávat výskyt spíše vysokých hodnot také u veličiny druhé.

Řekněme, že veličina X je snadno dostupná měření, zatímco veličina Y je naměřitelná jen s obtížemi- ať už technickými nebo ekonomickými. Lze dokázat, za použití principu nejmenších čtverců, že ze známé hodnoty x veličiny X se příslušná hodnota y veličiny Y nejlépe odhaduje pomocí lineární regresní funkce

, (3.11.2)

kde

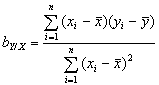(3.11.3)

je regresní koeficient veličiny Y na veličině X, a

(3.11.4)

je hodnota regresní přímky pro x = 0. Regresní přímka přitom prochází bodem o souřadnicích . Jak je patrno, , tj. nulová korelace X a Y, se graficky projeví rovnoběžností regresní přímky s vodorovnou osou souřadnou.

Pomocí korelačního koeficientu (3.11.1) je možno prověřovat hypotézu o nekorelovanosti veličin X a Y. K testování hypotézy r_XY = 0 lze využít Studentova t-testu, protože veličina vzniklá transformací

(3.11.5)

má t-rozdělení o n- 2 stupních volnosti.

Výpočet korelačního a regresního koeficientu ukážeme na příkladě.

Příklad. Z dílčích výsledků komunálních voleb v ČR konaných na podzim 1994 jsme se pokusili zachytit závislost některých ukazatelů volebního chování na vybraných ukazatelích sociální struktury. Jednotkou byly okresy; do studie bylo zahrnuto šest okresů střední a severní Moravy: Ostrava, Olomouc, Přerov, Bruntál, Šumperk, Opava.

Ukazatele sociální struktury byly tři:

Podíl vysokoškolsky vzdělaných obyvatel v populaci okresu
Podíl nezaměstnaných obyvatel v populaci okresu
Podíl obyvatel důchodového věku v populaci okresu

Jako ukazatele volebního chování jsme zvolili

Procentuální podpora ODS
Procentuální podpora KSČM

Data jsou shrnuta v tabulce

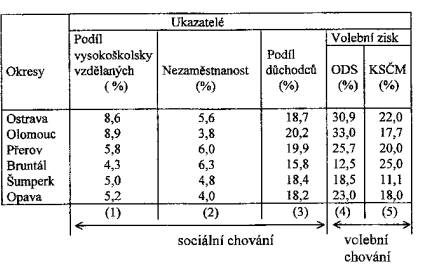
Předložená data (shromážděná studenty pro seminární práci) umožňují formulovat 6 úloh- kdy je hodnocena závislost vždy jednoho ze dvou ukazatelů volebního chování na jednom ze tří ukazatelů sociální struktury. Soubor zahrnuje pouze n = 6 prvků (okresů), což je příliš málo pro spolehlivou analýzu; Pearsonův korelační koeficient je poměrně značně citlivý na kolísání dat a při malém rozsahu výběru málo robustní.

Výpočty korelačních a regresních koeficientů a samozřejmě i průměrů a rozptylů byly provedeny s využitím statistického softwareového balíku STATGRAPHICS, v menu: Regression Analysis- Linear model. Výše korelačního (případně regresního) koeficientu svědčí o těsnosti vazby obou ukazatelů; je třeba ovšem mít na paměti, že někdy může jít i o vztah zprostředkovaný skrytou třetí veličinou, která jde paralelně s ukazatelem sociální struktury a „překrývá“ tak své vlastní působení působením zdánlivým.

Korelační diagramy naznačují, že

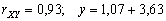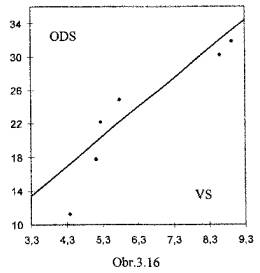
volební podpora ODS (Y) roste s rostoucím podílem X vysokoškolsky vzdělané populace; (viz Obr. 3.16)
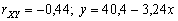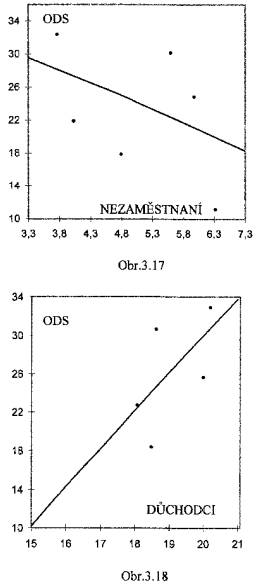
volební podpora ODS (Y) klesá s rostoucím podílem nezaměstnaných (X); (viz Obr.3.17)
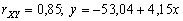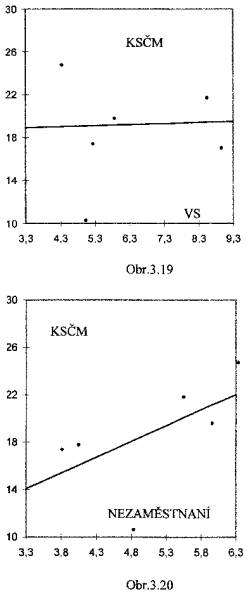
volební podpora ODS (Y) vzrůstá s vyšším podílem důchodců (X) v okrese; (viz Obr.3.18)
volební podpora KSČM (Y) na podílu vysokoškolsky vzdělaných (X) nezávisí; 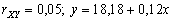(viz Obr.3.19)
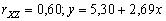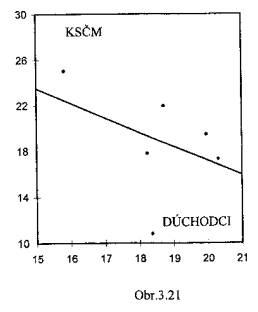
volební podpora KSČM (Y) roste s rostoucím podílem nezaměstnaných (X) v okrese; (viz Obr.3.20)
volební podpora KSČM (Y) klesá s rostoucím podílem důchodců (X) v okrese;

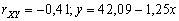
(viz Obr.3.21)

Rozhodování za nejistoty: princ Hamlet

„Žít či nežít“ to je oč tu běží;

zda je to ducha důstojnější snášet

střely a šípy rozkacené sudby,

či proti moři běd se chopit zbraně

a skoncovat je vzpourou. Zemřít-spát-

nic víc- a vědět, že tím spánkem končí

to srdce bolení, ta stará strast,

jež patří k tělu, to by byla meta

žádoucí nade všechno. Zemřít-spát-

Spát! Snad i snít? A v tom je právě háček!

To jaké sny by se nám mohly zdát

v tom spánku smrti, až se těla zbudem,

to, to nás zaráží. To je ten ohled,

jenž bídě s nouzí dává sto let žít.

Vždyť kdo by snášel bič a posměch doby,

sprostoty panstva, útlak samozvanců,

soužení lásky, nedobytnost práva,

svévoli úřadů a kopance,

jež od neschopných musí strpět schopný,

sám kdyby moh svůj propouštěcí list

si napsat třeba šídlem? Kdo by chroptě

se potil krví na galejích žití,

než jen, že strach z něčeho po smrti,

z těch krajů neobjevených, z nichž nikdo

se nevrací, nám ochromuje vůli

a dává snášet raděj zla, jež známe,

než prchnout k jiným, o nichž není zpráv?

Tak svědomí z nás ze všech dělá baby,

tak pomyšlením v nedokrevnou šeď

ruměnná svěžest odhodlání chřadne,

a podniky, jež mají spár a spád,

se pro ten ohled vychylují z dráhy

a tratí jméno skutku. Ale tiše!

Spanilá Ofélie! Vzpomeň dívko

v svých modlitbách mých hříchů všech.?

(Monolog Hamleta z 1. scény 3. dějství)

Kdyby měly být charakterizovány verše, které princ Hamlet tak vzrušujícím způsobem přednesl, jistě by při tom nechyběla slova jako „váhání“, „nejistota“, „rozhodování“.

Co je to vlastně rozhodování?

Rozhodujeme se neustále. Měli bychom tedy umět popsat to, co neustále děláme. I když bývá často méně obtížné něco udělat než vysvětlit, co se udělalo. A proč bylo uděláno právě to.

Princ Hamlet při svém rozhodování o tom, co by měl udělat, váhal. A přece víme, že bylo nakonec rozhodnuto. Dokonce tragicky. Vždycky se totiž všechno nějak rozhodne. J a k- to je, oč tu běží.

Co je to tedy rozhodování?

Poutník přijde na rozcestí, které mu dává možnost volby jedné z několika cest. Ví, kam chce dojít. Dále ví, že tam chce dojít cestou nejkratší. Snad je mu známo něco i o směru, kterým leží cíl jeho cesty. Tohle je ukázka situace rozhodování.

Základním prvkem její struktury je množina možných rozhodnutí, z nichž je třeba právě jedno si vybrat. (Takovým rozhodnutím je i možnost, že si poutník na rozcestí sedne pod strom a usne). Aby se mohl poutník racionálně rozhodnout, měl by kromě toho vědět něco o nákladech či výdajích nebo naopak o užitku či zisku té které volby. Jinak řečeno- měl by znát důsledky rozhodnutí.

A ještě něco.

Volba daného rozhodnutí nemusí vést k cíli jednoznačně. Naší strategií je zvolit rozhodnutí a na ni odpoví protihráč- řekněme Osud- ve hře zvané Život, svými vlastními strategiemi. O tom, kterou z možných strategií Osud na naši volbu odpoví, obvykle nemáme než více nebo méně nepřesný odhad. Formulovaný jako rozdělení pravděpodobností na množině možných strategií Osudu.

Za optimální se bude považovat takové rozhodnutí, pro které bude očekávaný zisk nejvyšší nebo náklady nejnižší. Očekávaný užitek dané cesty neboli matematická naděje užitku je přitom součinem užitku dané cesty a pravděpodobnosti jejího uskutečnění. Očekávaný užitek naší strategie je součtem očekávaných užitků všech cest, které mohou být tahem Osudu na tuto naši strategii.

Matematika se už před lety chopila pojmu „užitek“, vybudovala abstraktní teorii užitku a učinila ji součástí statistického rozhodování a teorie strategických her. Pokusme se teď rozpoznat některé rysy této teorie v úvahách prince dánského.

Podívejme se, dokáže-li chladný abstraktní model teorie užitku ve statistickém rozhodování, produkt 2. poloviny 20. století, alespoň do jisté míry popsat a analyzovat jednání prince Hamleta na hradě Elsinoru o několik set let dříve. Jednání, při němž šlo o život a smrt, o čest a podlost, lásku a nenávist, o moc, pomstu, beznaděj a zoufalství.

Konec konců, vždyť i Shakespearovo drama je- byť úchvatným- přece jen také pouze modelem jednání skutečných lidí v konkrétních společenských podmínkách. Schopnost vytvářet abstraktní modely je jedním z největších úspěchů lidského rozumu. A nezáleží na tom, Je-li skutečnost zobrazena dramatem nebo soustavou rovnic. Neskutečný příběh dánského krále Hamleta je už více než 300 let přesvědčivým důkazem strhující síly abstrakce.

Připomeňme si některé skutečnosti, podstatné pro naši analýzu.

Princi Hamletovi prozradí duch jeho zemřelého otce, že byl zrádně zabit svým bratrem Klaudiem, který se takto zmocnil trůnu i královny vdovy. Hamlet je rozhořčen a uvažuje o tom, co by měl učinit.

Jak jste to říkal princi?

„ Žít či nežít- to je oč tu běží;

zda je to ducha důstojnější snášet

střely a šípy rozkacené sudby,

či proti moři běd se chopit zbraně

a skoncovat je vzpourou. Zemřít--

Žít či nežít ...

To znamená, že princ uvažoval nad dvěma možnými strategiemi: nechat věcem volný průběh (žít) anebo spáchat sebevraždu.

Zdá se, že princ si přál zemřít ... Nemám pravdu?

„Zemřít- spát- spát!“

Ano, toužil jste po smrti jako záchraně od bolesti, svírající srdce. Pak jste zaváhal. Přepadly vás pochybnosti, zdali je tohle jediná možnost, kterou vám Osud může nabídnout poté, co si vezmete život ...

„Spát! Snad i snít? A v tom je právě háček!

To jaké sny by se nám mohly zdát

v tom spánku smrti, až se těla zbudem,

to, to nás zaráží. To je ten ohled,

jenž bídě s nouzí dává sto let žít.

Kdo by chroptě

se potil krví na galejích žití,

než jen, že strach z něčeho po smrti,

z těch krajů neobjevených, z nichž nikdo

se nevrací, nám ochromuje vůli

a dává snášet raděj zla, jež známe?

Ano, vyslovil jste to docela jasně.

Vašich veršů se nedotkla staletí. Nemůžeme jim proto nijak ublížit, pokusíme-li se vtěsnat jejich logiku do schématu rozhodovacího stromu

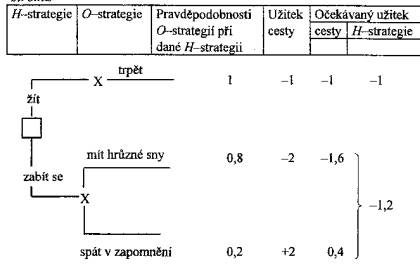
Na první strategii prince nabízí Osud jedinou strategii svoji. K jeho druhé alternativě však připouští dvě strategie vlastní.

Analýza situace předpokládá, že Hamlet jako rozhodující se subjekt má představu o pravděpodobnostech výskytu té které strategie Osudu a zároveň o užitku pro něj z cesty plynoucím.

Ve vašich verších žádná čísla nenajdeme. Dovolte nám proto překročit poněkud práh vašich úvah. Pokusíme se přitom neztratit jejich směr. Snad nám může být omluvou, že subjektivní ocenění užitku a pravděpodobností je pro nás stejně obtížné jako za vašich časů. I když jsme už stačili vytvořit k tomu účelu rozsáhlou metodiku psychologických měření.

Musíme kvantifikovat princovy představy o pravděpodobnostech, s nimiž mu Osud svoje řešení nabídne. Při rozhodnutí „Žít“ je to bez problémů: Osud nabízí jedinou strategii s pravděpodobností 1. Pokud by se princ rozhodl pro strategii „Zabít se“, nelze užitkovou funkci analyzovat bez toho, že by se odhadly možnosti výskytu obou strategií Osudu; řekněme, že je můžeme odhadovat v poměru 4:1, tj. 0,8 a 0,2.

Uvažujme pětibodovou škálu subjektivního užitku o stupních-2,-1, 0, 1, 2 a pokusme se vyjádřit princovy pocity čísly.

Uvážíme-li, jak vysoko kladně hodnotí Hamlet alternativu posmrtného klidu a naopak záporně život v utrpení či dokonce muka v očistci, byla snad naše volba užitku přiměřená.

Očekávaný užitek cesty se vypočítá jako součin užitku a podmíněné pravděpodobnosti příslušné strategie Osudu.

Očekávaný užitek princovy strategie se dostane sečtením očekávaných užitků všech cest, z princovy dané strategie vycházejících.

Tento poslední údaj je rozumným ukazatelem kvality princova rozhodnutí.

Jak je patrno, dávají obě princovy strategie zápornou hodnotu očekávaného užitku; s nevýraznou preferencí strategie “Žít“.

Pokusme se teď doplnit příběh další hypotetickou situací. Kromě strategií, o nichž Hamlet uvažoval, přicházela v úvahu alternativa další: „Zabít Klaudia“.

Lze předpokládat, že kdyby princ zvolil takovou strategii, nabídl by mu Osud jednu ze dvou strategií vlastních: buď by byl jeho čin pardonován a Hamlet- podle logiky věci- prohlášen králem, anebo by byl zabit jako královrah. Že byla prvá ze strategií Osudu opravdu možná, dokazují slova samotného Klaudia:

„Jak je nebezpečné, že je volný,

však dokročit naň podle práva nelze.

Je davem milován, jenž nesoudí.?

Posoudit výhodnost takové strategie můžeme ovšem jenom výpočtem očekávané užitkové funkce.

Všimněme si rozhodovacího schématu této strategie:

Připusťme, že Klaudiovo prohlášení dovoluje odhadnout Hamletovy šance v poměru 3:2. Při hodnocení užitku prvé cesty „Zabít Klaudia a přežít“ se můžeme opět opřít o text Hamletových veršů. Můžete nám připomenout, jak jste hodnotil bídu žití, princi?

„ Vždyť kdo by snášel bič a posměch doby,

sprostoty panstva, útlak samozvanců,

soužení lásky, nedobytnost práva,

svévoli úřadů a kopance,

jež od neschopných musí strpět schopný?

Ano, to jsou ta slova. Uvedl jste sedm důvodů, jež vám zprotivily žití. Jenomže ... jako král byste musel strpět z nich nejvýše dva ... řekněme „bič a posměch doby“ a „soužení lásky“. Jestliže tedy oněch sedm důvodů vedlo k užitku-1, můžeme připustit, že přítomnost pouhých dvou důvodů může způsobit zvýšení užitku (i když stále záporného) na-2/7 =- 0,286. Alternativě „Být zabit jako královrah“ je pak přiměřené přisuzovat maximálně negativní hodnocení-2. Za těchto okolností má Hamletova strategie „Zabít Klaudia“ očekávaný užitek- 0,971, o málo příznivější než strategie „Žít“, analyzovaná v předcházejícím schématu.

Zbývá ještě možnost pokusit se najít dodatečný zdroj informace, schopný snížit riziko, tj. pravděpodobnost výskytu nežádoucí strategie Osudu, totiž „Zabít královraha“.

Usoudili jsme, že s pravděpodobností 0,6 by Hamlet ušel trestu za královraždu. Protože bylo známo, že mezi venkovany má princ větší sympatie než v kruzích dvorní šlechty, oddané spíše Klaudiovi, jeví se výhodnou strategie „Zabít Klaudia“ tehdy, Je-li právě obklopen venkovany. Potřebovali bychom však přesnější výpočet, jak by tato modifikace princovy strategie ovlivnila očekávanou hodnotu užitkové funkce.

Připusťme, že by Hamlet využil hereckého představení a nechal provést anketu, zkoumající veřejné mínění v otázce „Jak naložit s princem, zavraždivším královského strýce?. Dejme tomu, že mezi těmi, kteří se přiklánějí k názoru „trestat královraha“ je 60% šlechticů a 40% venkovanů, zatímco mezi těmi, kteří by prince ušetřili, jsou dvořané i venkované zastoupeni stejným dílem.

Podmíněné pravděpodobnosti zastoupení sociální třídy mezi jedinci, vyslovujícími se pro zabití nebo pro ušetření prince, provinivšího se královraždou, shrnuje tabulka.

Odpověď	Dotazovaný byl
dotázaného	Šlechtic	Venkovan	å
Zabít prince	0,6	0,4	1
Ušetřit prince	0,5	0,5	1

Abychom mohli dovést výpočet do konce, zjednodušíme dále celou situaci předpokladem, že ve chvíli zabití Klaudia by byli přítomni buď jenom šlechtici nebo jenom poddaný lid.

V rozhodovacích schématech se často užívá tzv. Bayesova vzorce pro výpočet inverzních pravděpodobností. V uvažované situaci umožní tato metoda zpřesnit odhad výskytu osudových strategií: „Zabít prince“,-Ušetřit prince“. Těchto zpřesněných odhadů se pak znovu použije při výpočtu očekávaného užitku v rozhodovacím schématu.

Platí totiž vztahy

P(princ bude zabit| Klaudius je obklopen venkovany) =

P(princ bude zabit| Klaudius je obklopen šlechtici) =

Můžeme tedy propočítat užitkové funkce pro dvě princovy strategie, opírající se o dodatečnou informaci, totiž o zjištění, zda je Klaudius obklopen šlechtici nebo lidem.

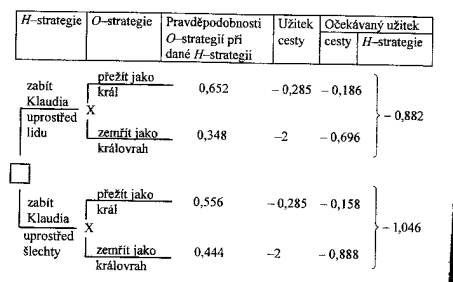
Výsledky naznačují, že dodatečná informace vnesla do rozhodování alespoň trochu nového světla: princ by měl uvažovat jako nejpříznivější (nejméně ztrátovou) strategii „Zabít Klaudia, obklopeného venkovany“. Náklady na průzkum veřejného mínění ovšem do užitkové funkce zakalkulovány nebyly.

Nedokážeme odhadnout, princi, zda by vás naše úvahy a výpočty dokázaly přesvědčit a ovlivnily by vaše jednání. Samozřejmě, na samém začátku vašeho příběhu- protože ve chvíli, kdy jste vy i Osud vyložili karty na stůl, není už o čem rozhodovat. Možná by nezískal vašeho ducha princip průměru, o nějž se- vědomě i nevědomky- tolik opíráme my dnes: nám připadá užitek málo pravděpodobné cesty k vysoce žádoucímu cíli stejný jako očekávaný užitek cesty vysoce pravděpodobné k cíli jen docela málo zajímavému.

Stejně jako za vašich časů i dnes každý z nás uspořádává životní hodnoty způsobem sobě vlastním: čest a slávu, moc, život i smrt. A jejich měření je pořád stejně obtížné.

Je nás dnes na světě víc než za vlády vašeho otce a strýce. Mnohem víc. Králové už dávno přestali rozhodovat. Řídíme společnost a výrobu pomocí vlád, ústavů a počítačů. Ani tak to není snadné a proto čas od času měníme pravidla rozhodování. Třeba dosazováním nových užitkových funkcí.

Naše metody statistického rozhodování nemohou zaručit, že by k tragédii vašeho rodu nedošlo. Jsme muži a nebudeme si nic namlouvat. To, co jsme se naučili navíc od vašich dob, je měření informace. Počítáme dnes rizika podobně jako pastýři vašeho otce počítali velikost svých stád. Hledáme postupy, zaručující rizika co nejmenší. Nedokážeme je odstranit; učíme se jim vyhýbat.

Tohle byste určitě pochopil, princi.

Protože i vy jste hledal.